细解奇门排盘心算法
第一步:要记住奇门3盘各元素的数字次序及排列次序
戊、己、庚、辛、壬、癸、丁、丙、乙,三奇六仪对应:
1、2、3、4、5、6、7、8、9;
休、死、伤、杜、中、开、惊、生、景,9门对应:
1、2、3、4、5、6、7、8、9;
蓬、芮、冲、辅、禽、心、柱、任、英,9星对应:
1、2、3、4、5、6、7、8、9;
符、蛇、阴、六、白、玄、地、天,8神对应:
1、2、3、4、5、6、7、8。
8门的排列次序:休、生、伤、杜、景、死、惊、开,依次环排8宫;
9星的排列次序:蓬、任、冲、辅、英、芮(禽)、柱、心,依次环排8宫;
8神的排列次序:符、蛇、阴、六、白、玄、地、天,依次环排8宫。
第二步:迅速判断时辰所在旬甲子(戊)旬、甲戌(己)旬、甲申(庚)旬、甲午(辛)旬、甲辰(壬)旬、甲寅(癸)旬;分别对应数字:1,2,3,4,5,6;
十天干分别对应1 至 10 的数字;
十二地支分别对应:1 到 12 的数字;
在判断前先要记住:60甲子共分6旬,每旬分别对应数字:0,10,8,6,4,2 比如:丙辰时要知道在哪一旬,天干丙为3,地支辰为5,地支数5减天干数3等于2,故知丙辰时在第6旬,也就是时在甲寅(癸)旬;又如丙子时,丙为3,子为1,1-3= -2,这时得出的数字小于0,怎么办?那就加上12吧!结果为10,故知为第2旬,甲戌(己)旬,这里特别要说明,知道时辰在哪个旬很重要得,奇门排盘所求直符关键就在此!
总结公式如下:旬数对应数=地支数-天干数如果旬数对应数小于0就再加上12,为最终旬数对应数,如结果为0就是甲子旬,为10就是甲戌旬,依次类推。
第三步:根据用局数求直符和直使先看看阳遁直符和直使的求法:直符直使序数=所用局数+时辰所在旬序数 – 1 如果直符直使序数结果大于9,那么就再此基础上减去9,即为最终次序数。如果:序数=1,那么直符为天蓬,直使为休门;为2时,直符为天芮,直使为死门,依次类推。再看看阴遁直符和直使的求法:直符直使序数=1+所用局数-时辰所在旬序数如果直符直使序数结果大于9,那么就再此基础上减去9,即为最终次序数。如果:序数=1,,那么直符为天蓬,直使为休门,依次类推。
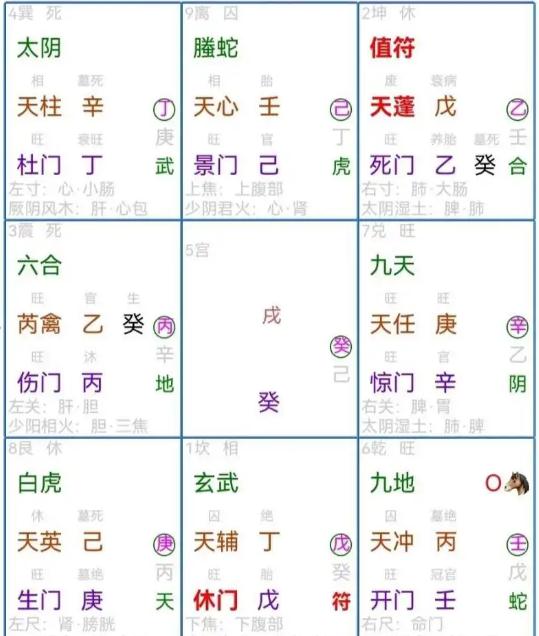
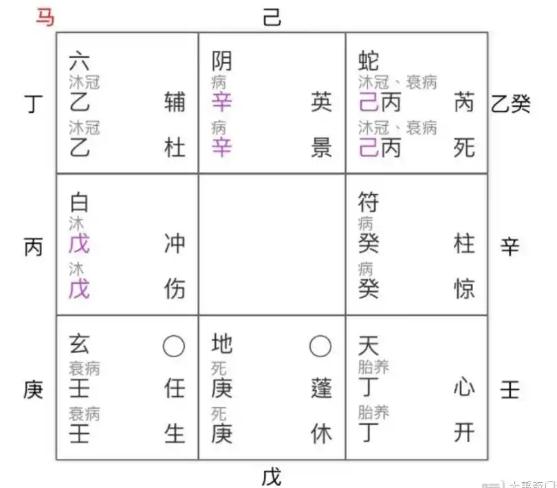
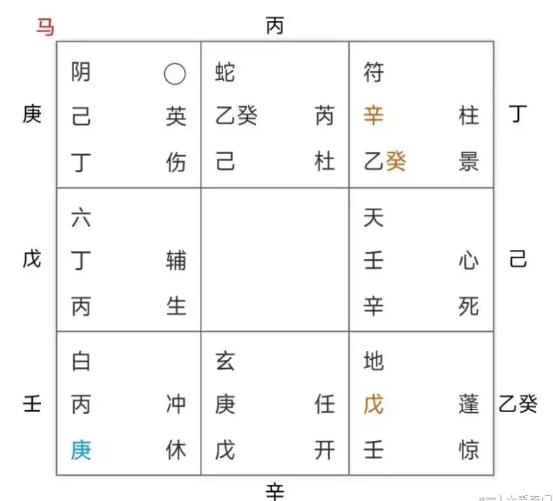
第四步:求直符直使落宫(书中36页的内容,几个公式就解决了)阳遁时的求法:直符落宫数=时干在三奇六仪中所对应的次序数+局数-1如果落宫数>9,那么就在此基础上减去9,即为最终所得的直符落宫数,如果落宫数<0,那么就在此基础上加上9,即为最终所得的直符落宫数。阴遁时的求法:直符落宫数=1+局数-时干在三奇六仪中所对应的次序数如果落宫数9,那么就在此基础上减去9,即为最终所得的直符落宫数。举例1:如阳遁7局,乙丑时,求直符及落宫乙在10天干中对应2,丑在12地支中对应2 2-2=0,知道乙丑为甲子旬,旬序数为1。直符直使序数=所用局数+时辰所在旬序数 – 1 =7+1-1=7 知7对应7宫的天柱和惊门,既天柱和惊门为直符和直使;直符落宫数=局数 - 时辰所在旬序数+时干在三奇六仪中所对应的次序数 =7-1+9=15 15超过了9,所以此处减去9等于6,既知直符落于6宫。举例2:如阴遁6局,辛丑时,求直符及落宫辛在10天干中对应8,丑在12地支中对应2 2-8=-6,小于0。所以-6再加上12等于6,知道辛丑为甲午旬,旬序数为4。直符直使序数=1+所用局数-时辰所在旬序数 =1-(-6)-4=3,结果为3,故知3对应宫的天冲和伤门为直符和直使。直符落宫数=1+局数-时干在三奇六仪中所对应的次序数 =1+6-4=3,所以直符落宫为3宫以上不分阴阳遁,如逢天禽为直符那么,天禽皆随天芮走宫,以死门为直使。
第五步:求直使落宫阳遁时的求法:时干在十天干中序数:甲1、乙2、丙3,依次顺类推直使落宫=直使序数+时干在十天干中序数-1如结果大于9,既减去9为直使落宫数。阴遁时的求法:时干在十天干中序数:甲1、乙9、丙8,依次逆类推直使落宫=直使序数+时干在十天干中序数-1如结果大于9,既减去9为直使落宫数。以上不分阴阳遁,如果直使落中5宫皆寄坤2宫。如1:阳遁7局,乙丑时 天柱和惊门为直符和直使 求直使落宫直使落宫=直使序数+时干在十天干中序数-1 =7+2-1=8,所以此时直使惊门落8宫。如2:阴遁6局,辛丑时,求直使及落宫 天冲和伤门为直符和直使。直使落宫=直使序数+时干在十天干中序数-1 =3+3-1=5,所以此时直使惊门落5宫寄坤2宫。
以上五步内容为必须记住的东西,三式盘面的各元素对应的数字,以及在某种条件下,数字要顺逆对应,如求直使的时候十天干的对应次序数阳遁和阴遁是不同的。要分清十天干的对应次序数,和三奇六仪的对应序数。
新安钓叟-颂曰:
天地人我一掌中,宇宙旋转妙法通,三奇六仪为我用,四面八方任纵横。不食人间半点尘,烟波万顷一闲身。一篮鱼换一壶酒,懒向桃源去问津。














 教学堂
教学堂 社区
社区 发现
发现 开运
开运 景观件
景观件 探索发现
探索发现 






